在现代工业领域,特别是高可靠性要求的电子设备、航空航天及新能源系统中,产品寿命往往远超常规试验验证周期。加速退化试验(ADT) 作为一种高效评估产品长期可靠性的关键技术,通过施加高于正常水平的应力条件加速产品退化过程,并基于退化数据模型外推产品在正常使用条件下的寿命与可靠性指标。本文将以铝电解电容这一关键电子元件为具体案例,系统阐述基于加速退化试验数据的可靠性分析方法与实践流程。
一、 理论基础:加速退化试验与可靠性建模
核心概念:
退化 (Degradation): 产品性能参数随时间推移而发生的渐变劣化过程(如电容容量衰减、机械部件磨损、材料强度下降等)。
性能阈值 (Failure Threshold): 产品性能退化到某一临界值时即判定为失效。该阈值通常基于功能需求或行业标准设定(如电容容量降至初始值的80%)。
加速退化试验 (ADT): 在高于正常水平的单一或多个应力(如温度、电压、湿度、机械载荷、电流)下进行试验,加速产品的退化过程,在较短时间内获得退化数据。
加速模型 (Acceleration Model): 建立应力水平与退化速率(或失效时间)之间定量关系的物理或统计模型。它是将加速应力下的试验结果外推至正常应力水平的关键桥梁。
退化轨迹模型 (Degradation Path Model): 描述单个产品性能参数随时间(或使用量)变化的数学模型(如线性、指数、幂律模型、随机过程模型如Wiener过程、Gamma过程)。
关键模型:
线性模型: D(t) = β0 + β1 * t + ε。适用于退化速率相对恒定的情况。
指数模型: D(t) = β0 * exp(β1 * t) + ε 或 ln(D(t)) = ln(β0) + β1 * t + ε。适用于退化速率与当前退化量成比例的情况(如化学反应、扩散过程)。
幂律模型: D(t) = β0 * t^β1 + ε。
随机过程模型 (Wiener过程): D(t) = μ * t + σ * W(t),其中μ为漂移系数(平均退化速率),σ为扩散系数(表征退化波动),W(t)为标准布朗运动。能有效描述退化路径的随机波动性。
Arrhenius模型: 描述温度对化学反应速率(如电解液蒸发、氧化膜生长)的影响。速率常数 K ∝ exp(-Ea / (k * T)),其中Ea为激活能,k为玻尔兹曼常数,T为绝对温度。
Eyring模型: 更广义,可包含温度和湿度、电压等其他应力。
逆幂律模型 (Inverse Power Law - IPL): 描述电压、机械应力、电流等与寿命的关系。寿命 L ∝ S^(-n),其中S为应力水平,n为加速因子。
Peck模型: 常用于描述温湿度综合应力(温湿度加速试验)。
物理-经验加速模型:
退化轨迹模型:
可靠性指标:
可靠度函数 R(t): 产品在时间t仍能正常工作的概率。
累积失效分布函数 F(t): 产品在时间t前失效的概率,F(t) = 1 - R(t)。
概率密度函数 f(t): 失效时间分布的概率密度。
平均失效前时间 (MTTF) / 平均寿命: 失效时间的期望值。
百分位寿命 (B_p): 可靠度下降到p%时对应的时间(如B10寿命表示10%产品失效的时间,常作为设计寿命目标)。
二、 案例研究:铝电解电容寿命评估
研究对象与背景:
器件: 某型号铝电解电容,标称容量C0=1000μF,额定电压Vr=25V,额定温度Tr=105°C。
退化机理: 铝电解电容的主要失效模式是容量衰减和内阻(ESR)增大。容量衰减主要由电解液通过密封橡胶逐渐挥发损失以及阳极氧化铝介质层劣化导致。
性能参数与阈值: 选择电容量 (C) 作为关键退化参数。失效阈值设定为初始容量C0的80%,即当C ≤ 0.8 * C0 = 800μF时判定为失效。此阈值是电子行业的常用标准(如IEC 60384-4)。
目标: 评估该电容在额定工作条件(温度Tuse=65°C, 电压Vuse=20V)下的B10寿命(10%失效时间)和MTTF。
加速退化试验设计:
温度应力 (T): 105°C (额定温度,作为参考点),115°C,125°C。避免过高温度引入非主导失效机理。
电压应力 (V): 25V (额定电压),30V,35V。
应力组合: 采用3 (温度) x 3 (电压) = 9个加速应力组合。每个应力组合下放置10个样本。
正常应力: Tuse=65°C, Vuse=20V。
加速应力选择: 根据退化机理,选择温度(T) 和工作电压(V) 作为加速应力。高温加速电解液挥发和化学反应;高电压加速阳极氧化膜劣化(电场作用)。
应力水平设置:
测量方案: 在试验开始(t=0),以及24h, 48h, 100h, 200h, 500h, 1000h, 1500h, 2000h时,将电容取出冷却至室温(如25°C),测量其电容量C。记录每个样本在每个测量时间点的容量值。
试验终止: 当大部分样本在最高应力水平(125°C/35V)下容量衰减至阈值800μF以下时终止试验(约2000h)。
试验数据示例 (模拟数据):
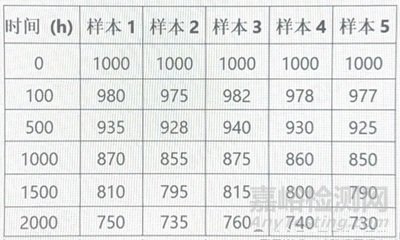
下表展示了在应力组合T=125°C, V=35V下,5个样本的部分容量测量数据(单位:μF):
数据分析与建模:
步骤1:退化轨迹建模 (个体层面)
观察不同应力水平下的退化数据,发现电容容量随时间呈现近似指数衰减趋势。因此,对每个样本i在应力组合(Tj, Vk)下的退化路径,采用指数退化模型:
C_{ijk}(t) = \beta_{0ijk} \cdot exp(-\beta_{1ijk} \cdot t) + \varepsilon_{ijk}(t)
或等价地对两边取自然对数,转化为线性模型:
ln(C_{ijk}(t)) = ln(\beta_{0ijk}) - \beta_{1ijk} \cdot t + \varepsilon_{ijk}(t) \quad \text{即} \quad y_{ijk}(t) = \alpha_{ijk} - \beta_{1ijk} \cdot t + \varepsilon_{ijk}(t)
其中:
C_{ijk}(t)是样本i在应力(Tj, Vk)下时间t的容量。
β0ijk (或αijk = ln(β0ijk)) 可视为初始容量的随机波动(通常接近标称值1000)。
β1ijk 是退化速率常数,是模型的核心参数,反映退化的快慢。
ε_{ijk}(t) 是随机测量误差或微小波动,通常假设独立同分布,服从N(0, σ_ε^2)。
使用最小二乘法(OLS) 或最大似然法(MLE) 对每个样本的退化路径独立拟合,估计其αijk和β1ijk。假设对样本1在(125°C, 35V)下的拟合结果为:β1_1,125,35 ≈ 0.00025 h⁻¹(意味着容量以约每小时0.025%的初始值衰减)。
步骤2:建立加速模型 (退化速率 vs 应力)
核心目标是建立退化速率常数β1 与温度T 和电压V 的关系。根据物理机理:
温度T的影响符合Arrhenius模型。
电压V的影响符合逆幂律模型(IPL)。
因此,采用组合加速模型:
\beta_1(T, V) = A \cdot V^n \cdot exp\left(-\frac{E_a}{k \cdot T}\right)
其中:
A 是常数。
n 是电压加速因子。
Ea 是激活能 (eV)。
k 是玻尔兹曼常数 (8.617333262145 × 10^{-5} eV/K)。
T 是绝对温度 (K)。
对上述模型两边取自然对数,转化为线性形式:
ln(\beta_1) = ln(A) + n \cdot ln(V) - \frac{E_a}{k} \cdot \frac{1}{T}
令:
Y = ln(β1)
X1 = ln(V)
X2 = 1/T
β0 = ln(A)
β1_coef = n (注意:此β1_coef是线性模型的系数,不同于退化速率β1)
β2_coef = -Ea / k
则模型变为:
Y = β0 + β1_coef \cdot X1 + β2_coef \cdot X2 + \delta
其中δ为随机误差。
收集所有样本在所有加速应力组合下拟合得到的β1ijk值及其对应的V和T。使用多元线性回归(MLR) 拟合上述模型,估计参数β0, β1_coef (n), β2_coef,进而得到A = exp(β0), n = β1_coef, Ea = -β2_coef * k。
假设拟合结果示例:
n ≈ 3.5 (电压加速因子)
Ea ≈ 0.85 eV (激活能)
A ≈ 1.2e8 (常数)
步骤3:外推正常应力下的退化速率
将正常使用应力Tuse=65°C=338K, Vuse=20V代入建立的组合加速模型:
\beta_{1, normal} = A \cdot (Vuse)^n \cdot exp\left(-\frac{E_a}{k \cdot Tuse}\right)
代入上述假设参数:
\beta_{1, normal} ≈ 1.2e8 \cdot (20)^{3.5} \cdot exp\left(-\frac{0.85}{8.617e-5 \cdot 338}\right) ≈ 1.2e8 \cdot 160000 \cdot exp(-29.85) ≈ 1.92e13 \cdot 1.58e-13 ≈ 3.03e-6 \text{ h}^{-1}
计算得到正常使用条件下的平均退化速率常数β1,normal ≈ 3.03e-6 h⁻¹。
步骤4:计算伪失效时间 & 构建寿命分布
确定失效阈值: D_f = 0.8 * C0 = 800μF。
计算每个样本的伪失效时间: 利用每个样本在加速应力下拟合得到的退化轨迹模型C(t) = β0i exp(-β1i t),令C(t) = D_f,求解时间t:
t_{fi} = \frac{1}{\beta_{1i}} \cdot ln\left(\frac{\beta_{0i}}{D_f}\right)
由于β0i通常接近C0,且ln(β0i/D_f) ≈ ln(C0 / (0.8*C0)) = ln(1.25) ≈ 0.223,因此t_fi主要取决于1/β1i。对于在应力(Tj, Vk)下的样本,其伪失效时间t_fijk反映了该应力水平下的“寿命”。
转换到正常应力下的伪失效时间: 利用加速模型β1 ∝ f(T, V)(即β1,stress / β1,normal = [f(Tstress, Vstress) / f(Tnormal, Vnormal)])。因此,正常应力下的等效失效时间t_{f, normal, ijk}为:
t_{f, normal, ijk} = t_{f, ijk} \cdot \frac{\beta_{1, stress, ijk}}{\beta_{1, normal}}
其中β1,stress,ijk是该样本在加速应力下拟合得到的退化速率,β1,normal是步骤3计算出的正常应力下的平均退化速率。关键点: 此步骤利用加速模型和个体退化速率,将不同加速应力下观测到的伪失效时间,统一外推到正常应力水平下,得到一组“等效”的正常工作条件下的失效时间数据{t_{f, normal, ijk}}。
构建寿命分布: 收集所有样本在所有加速应力下转换得到的t_{f, normal, ijk}值(本例共9 stress x 10 samples = 90个数据点)。分析这些数据,拟合合适的寿命分布模型(如Weibull分布、Lognormal分布)。假设数据服从双参数Weibull分布:
F(t) = 1 - exp\left(-\left(\frac{t}{\eta}\right)^{\beta}\right)
其中η是尺度参数(特征寿命),β是形状参数。使用MLE或概率图法估计η和β。
假设拟合结果: η ≈ 95,000 小时, β ≈ 2.1。
可靠性评估结果:
可靠度函数:
R(t) = exp\left(-\left(\frac{t}{95000}\right)^{2.1}\right)
B10寿命: 解方程R(B10) = 0.9:
0.9 = exp\left(-\left(\frac{B10}{95000}\right)^{2.1}\right) => \left(\frac{B10}{95000}\right)^{2.1} = -ln(0.9) ≈ 0.10536 => \frac{B10}{95000} = (0.10536)^{1/2.1} ≈ 0.485 => B10 ≈ 46, 100 \text{ 小时}
MTTF: 对于Weibull分布,MTTF = η * Γ(1 + 1/β)。Γ(1 + 1/2.1) ≈ Γ(1.476) ≈ 0.886 (查Γ函数表)。因此:
MTTF ≈ 95, 000 * 0.886 ≈ 84, 170 \text{ 小时}
结果解释: 在65°C、20V的额定工作条件下,该型号铝电解电容的B10寿命(10%失效时间)预计约为46, 100小时(约5.26年),平均失效前时间(MTTF)约为84, 170小时(约9.6年)。Weibull形状参数β=2.1>1表明失效具有明显的耗损特性,早期失效风险较低,但随着使用时间增长,失效概率逐渐增加。
三、 方法优势、挑战与工程应用
优势:
高效性: 显著缩短试验周期,在较短时间内获得产品长期可靠性信息。
信息量丰富: 利用整个退化过程数据,比仅记录失效时间的试验提供更多信息,尤其适用于高可靠性产品。
适用于多种失效模式: 能处理性能渐变导致的失效。
可预测性: 建立明确的退化物理模型和加速模型,预测结果更具物理意义和说服力。
小样本潜力: 结合随机过程模型和贝叶斯方法,可在一定程度上缓解小样本问题。
挑战与注意事项:
主导失效机理一致性: 加速应力下诱发的失效机理必须与正常使用条件下的主导失效机理一致。否则,外推结果无效。需通过失效分析(如解剖、SEM、电镜)验证。
加速模型准确性: 模型选择和参数估计的准确性直接影响外推结果的可靠性。物理模型优于纯统计模型。
退化轨迹模型选择: 选择能准确描述实际退化过程的模型至关重要。模型误设会导致系统偏差。
测量误差与波动: 退化测量中的噪声和个体差异需要在模型中考虑(如随机效应、随机过程)。
样本量: 虽然信息量丰富,但足够的样本量仍是保证统计显著性的基础,尤其是在多应力加速试验中。
外推风险: 从高应力外推到低应力(尤其是温度)存在不确定性,外推幅度越大,风险越高。应力水平设置应尽量接近实际使用条件上限。
工程应用价值:
产品设计与改进: 识别关键退化参数和敏感应力,指导设计优化(如选择更稳定的电解液、改进密封工艺、优化散热)。
寿命预测与保修制定: 为产品提供定量的寿命指标(B10, MTTF),支撑保修期设定和备件计划。
可靠性验收试验(RQT): 基于ADT模型设计高效的验收方案,验证批量产品是否达到可靠性目标。
筛选与老化: 利用ADT结果优化筛选应力条件和时间(如高温老化),剔除早期失效品。
状态监测与预测性维护: 理解关键性能参数的退化规律,为在线监测和剩余寿命预测(RUL)提供模型基础。
供应链管理: 评估不同供应商或批次产品的可靠性差异。
四、 结论
基于加速退化试验数据的可靠性分析,通过深入挖掘性能参数渐变过程中蕴含的信息,结合物理机理驱动的加速模型,为评估高可靠性、长寿命产品的寿命和可靠性指标提供了一条高效且强有力的技术途径。本文以铝电解电容为具体案例,详细展示了从试验设计、数据采集、退化轨迹建模、加速模型建立、外推到正常条件、寿命分布拟合到最终可靠性指标计算的完整流程。
该方法的核心价值在于其物理意义明确和预测能力强大。然而,其成功应用高度依赖于对产品失效机理的深刻理解、加速模型的合理选择与验证、退化轨迹的准确描述以及严谨的数据分析。工程师必须清醒认识到加速应力下失效机理一致性这一关键前提和外推的不确定性。克服这些挑战,基于ADT的可靠性分析将成为支撑产品高可靠性设计、验证与保障不可或缺的利器,在航空航天、新能源、高端装备制造、医疗器械等领域发挥越来越重要的作用。
案例启示: 对于案例中的铝电解电容,设计工程师可依据预测的B10寿命(约5.26年)评估其在目标设备(如光伏逆变器预期寿命20年)中的适用性。若寿命不足,可考虑选择更高额定温度(如125°C)的电容、优化散热设计以降低实际工作结温、或采用电压降额设计(如工作在16V而非20V),并重新进行ADT评估其效果。制造商也可依据MTTF制定合理的保修政策(如5年保修)。该分析结果为产品全生命周期的可靠性决策提供了坚实的量化基础。