在产品研发中，可靠性是决定成败的关键要素之一。尤其在航天、汽车、医疗设备等高要求领域，系统可靠性指标的科学分配更是设计流程的核心环节。本文将系统阐述可靠性指标分配的理论方法、实施步骤，并结合卫星电源系统案例进行深度解析，为工程实践提供参考。

 

一、可靠性指标分配的本质与价值

可靠性指标分配（Reliability Allocation）是将系统级可靠性目标（如任务可靠度Rs、平均无故障工作时间MTBF）科学分解到各子系统、单元或组件的过程。其核心价值在于：

设计指导性：为各层级设计人员提供明确的可靠性目标，引导设计、选型和验证；

资源优化：识别关键单元，聚焦资源解决薄弱环节，避免“过度设计”或“设计不足”；

风险可控性：早期暴露潜在故障点，支持风险管理和设计迭代；

量化管理基础：为可靠性预计、测试方案制定提供输入，实现全过程量化管控。

 

二、可靠性分配的核心方法

选择合适的方法取决于系统复杂度、可用数据及设计阶段。以下是常用方法：

等分配法 (Equal Allocation)

原理：假设所有单元对系统可靠性贡献相同且相互独立（串联系统）。

公式：对于n个单元串联的系统，要求系统可靠度Rs，则单元目标可靠度Ri = Rs^(1/n)。

优点：简单直观。

缺点：忽略单元复杂度、成本、技术难度差异，结果常不合理。仅适用于概念设计初期或高度相似单元。

评分分配法 (ARINC, AGREE Comprehensiveness)

确定评分因素及其权重(Wj)。

为每个单元i对每个因素j评分(Cij，通常1-10分，分数越高越不利)。

计算单元i的综合评分因子Ki = Σ(Wj * Cij) / Σ(Wj * Cmax_j)。

分配指标：Ri = 1 - Ki * (1 - Rs) / Σ(Ki) （串联系统近似）。

原理：基于专家经验，对影响单元可靠性目标的关键因素（复杂度、技术成熟度、环境严酷度、维修性、重要性）进行评分加权。

步骤：

优点：考虑多种工程因素，相对合理，易于操作。

缺点：依赖专家经验，主观性较强。

比例组合法 (Feasibility of Objectives)

原理：根据单元现有可靠性水平（预计值或历史数据）、技术提升潜力、改进成本等因素，按比例分配系统可靠性提升的“负担”。

公式：Ri = R_baseline_i + λi * (Rs - ΠR_baseline_i)。λi是分配因子，反映单元i承担改进责任的权重 (Σλi = 1)。

优点：结合现状与潜力，更贴近工程实际。

缺点：需要较准确的基线数据。

AGREE 分配法 (AGREE Reliability Allocation - 核心推荐)

单元失效率分配： λi = [Ci * (-ln Rs)] / [Ei * Σ(Cj / Ej)]

单元可靠度分配： Ri(t) = exp(-λi * t)

其中：

λi：分配给单元i的失效率目标

Ci：单元i的复杂度因子（如标准元件数量）

Ei：单元i的重要性因子（单元i故障导致系统失效的概率，0<Ei≤1）

Rs：系统任务可靠度目标（任务时间t内）

t：任务时间

Σ(Cj / Ej)：对所有单元求和

原理：美国电子设备可靠性咨询组(AGREE)提出，综合考虑单元复杂度（元器件数量/类型）和重要性（故障导致系统失效的概率）。适用于电子设备为主的系统。

公式：

优点：逻辑清晰，量化程度高，在电子/电气系统广泛应用。

缺点：对机械、结构件适用性稍弱；需准确评估Ci和Ei。

 

三、可靠性指标分配实施流程

明确系统定义与边界：

清晰定义系统功能、组成结构（分解到可分配层级）。

绘制可靠性框图(RBD)，明确单元间可靠性逻辑关系（串联、并联、冗余等）。

确定顶层可靠性指标：

获取并确认系统级可靠性要求（Rs, MTBF等）及任务剖面（时间、环境）。

选择分配方法：

根据系统特点、数据可用性、设计阶段选择最合适的方法（常组合使用）。

收集与分析输入数据：

单元信息：功能、复杂度（元器件数、图纸页数、代码行数等）、技术成熟度。

环境信息：各单元所处环境严酷度。

重要性信息：单元故障对系统功能/安全的影响（FMEA/FMECA结果）。

历史/预计数据：类似单元可靠性数据、初步预计值。

约束条件：成本、重量、体积、功耗限制。

执行分配计算：

应用选定的方法和公式进行计算。

迭代过程：初步分配结果需评估技术可行性、成本效益。对不合理指标（过高或过低）进行调整，可能需重新分配或反馈调整系统目标。

形成分配报告与确认：

清晰记录分配方法、假设、输入数据、计算结果、最终分配的指标。

获得相关设计、工程、管理人员的评审与确认。

动态跟踪与更新：

随着设计深入、测试数据产生、设计变更，需重新评估和更新分配结果，确保其始终有效指导设计。

 

四、实战案例：某低轨遥感卫星电源系统可靠性分配

系统目标：卫星设计寿命5年，要求任务末期（5年）电源系统可靠度Rps ≥ 0.98。

系统描述：采用太阳电池阵-蓄电池组联合供电方案（SAPS），核心单元包括：

太阳电池阵 (SAA)：产生电能。

电源控制器 (PCU)：调节、分配、控制电能（含MPPT、充放电控制）。

锂离子蓄电池组 (BAT)：存储能量，供阴影期或峰值功率使用。

配电器 (PDU)：将母线电压分配到各负载。

可靠性框图：SAA, PCU, BAT, PDU 串联工作，任一失效将导致电源系统失效。[SAA] -- [PCU] -- [BAT] -- [PDU]

分配方法选择：系统以电子设备为主，采用AGREE分配法。复杂度(Ci)用“标准元器件等效数”衡量，重要性(Ei)基于功能分析确定（假设均为关键单元，Ei=1）。

数据收集与评估：

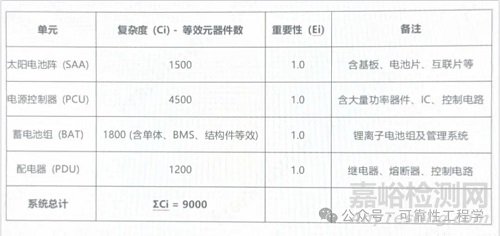
分配计算 (AGREE法)：

R_SAA(5) = exp(-0.003367 * 5) ≈ exp(-0.016835) ≈ 0.9833

R_PCU(5) = exp(-0.010102 * 5) ≈ exp(-0.050510) ≈ 0.9507

R_BAT(5) = exp(-0.004040 * 5) ≈ exp(-0.020200) ≈ 0.9800

R_PDU(5) = exp(-0.002693 * 5) ≈ exp(-0.013465) ≈ 0.9866

λ_SAA = [1500 * 0.020203] / [1 * 9000] ≈ 0.003367 / 年 (MTBF ≈ 297 年)

λ_PCU = [4500 * 0.020203] / [1 * 9000] ≈ 0.010102 / 年 (MTBF ≈ 99 年)

λ_BAT = [1800 * 0.020203] / [1 * 9000] ≈ 0.004040 / 年 (MTBF ≈ 247.5 年)

λ_PDU = [1200 * 0.020203] / [1 * 9000] ≈ 0.002693 / 年 (MTBF ≈ 371 年)

系统目标：Rps(5年) = 0.98， 故 -ln(Rps) = -ln(0.98) ≈ 0.020203

计算分配因子分母：Σ(Cj / Ej) = (1500/1) + (4500/1) + (1800/1) + (1200/1) = 9000

分配各单元5年任务失效率λi：

计算各单元5年可靠度目标Ri(5)：

验证系统可靠度：Rps_calc = R_SAA * R_PCU * R_BAT * R_PDU ≈ 0.9833 * 0.9507 * 0.9800 * 0.9866 ≈ 0.9000 << 0.98! 计算错误？

问题发现与修正：

上述计算错误在于混淆了失效率λi和任务可靠度Ri(t)的关系。AGREE公式直接分配的是失效率λi，单元任务可靠度Ri(t) = exp(-λi * t)。

验证系统可靠度应为：Rps_calc = exp(-(λ_SAA + λ_PCU + λ_BAT + λ_PDU) * 5) = exp(-(0.003367 + 0.010102 + 0.004040 + 0.002693) * 5) = exp(-0.020202 * 5) = exp(-0.10101) ≈ 0.9040。仍然远低于0.98！

错误根源：AGREE原始公式适用于恒定失效率（指数分布）和串联系统，其分配结果应满足 Σλi = -ln(Rs)/t。本例中 -ln(0.98)/5 ≈ 0.0040406 /年，而我们分配的总失效率 Σλi ≈ 0.020202 /年，是目标的5倍！问题出在公式理解错误。

正确应用AGREE公式：

R_SAA(5) = exp(-0.0006734 * 5) ≈ exp(-0.003367) ≈ 0.9966

R_PCU(5) = exp(-0.0020202 * 5) ≈ exp(-0.010101) ≈ 0.9899

R_BAT(5) = exp(-0.0008081 * 5) ≈ exp(-0.0040405) ≈ 0.9960

R_PDU(5) = exp(-0.0005387 * 5) ≈ exp(-0.0026935) ≈ 0.9973

分母 Σ(Cj / Ej) = 9000 (不变)

λi = [Ci * (-ln(0.98))] / [Ei * 5 * Σ(Cj / Ej)] = [Ci * 0.020203] / [1 * 5 * 9000] = [Ci * 0.020203] / 45000

λ_SAA = (1500 * 0.020203) / 45000 ≈ 0.0006734 /年 (MTBF ≈ 1485 年)

λ_PCU = (4500 * 0.020203) / 45000 ≈ 0.0020202 /年 (MTBF ≈ 495 年)

λ_BAT = (1800 * 0.020203) / 45000 ≈ 0.0008081 /年 (MTBF ≈ 1237 年)

λ_PDU = (1200 * 0.020203) / 45000 ≈ 0.0005387 /年 (MTBF ≈ 1856 年)

Σλi ≈ 0.0006734 + 0.0020202 + 0.0008081 + 0.0005387 = 0.0040404 /年 (等于 -ln(0.98)/5，正确！)

AGREE分配公式应为：λi = (Ci * (-ln Rs)) / (Ei * t * Σ(Cj / Ej)) 注意分母中有任务时间t！

重新计算：

计算各单元5年可靠度目标Ri(5)：

验证系统可靠度：Rps_calc = R_SAA(5) * R_PCU(5) * R_BAT(5) * R_PDU(5) ≈ 0.9966 * 0.9899 * 0.9960 * 0.9973 ≈ 0.9800 (符合目标Rps=0.98)

结果分析与工程迭代：

设计强化：PCU采用更高等级(如QML-V或S级)元器件、更健壮的降额设计、关键功能冗余（如双备份控制器）。

重新评估：若初步设计分析表明原PCU设计难以达到0.9899，需反馈：

论证是否可略微降低Rps目标（如0.975）？

是否可优化系统架构，引入部分冗余提高系统可靠度，从而放松对PCU的要求？

是否需显著增加PCU研发投入？需进行成本-效益分析。

PCU单元分配到的失效率最高(λ_PCU ≈ 0.00202/年， R_PCU(5)≈0.9899)，远低于其他单元。这与其最高复杂度(Ci=4500)相符，表明它是系统的可靠性瓶颈。

工程挑战：太空环境下5年MTBF≈495年对高复杂度PCU极具挑战（需考虑辐射、热循环、真空等效应）。

迭代措施：

SAA/BAT/PDU目标相对宽松，但仍属高要求，需精心设计和验证。BAT需特别关注锂离子电池的长寿命和深放电管理策略。

分配结果确认与输出：

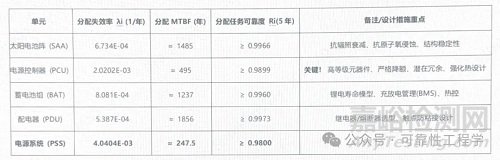
此表成为各分系统设计师的可靠性设计目标和后续预计、测试的基准。

 

五、可靠性分配的关键成功要素与挑战

早期启动与迭代： 分配是动态过程，需在方案阶段启动，并随设计深入反复迭代更新。

多学科协同： 需设计、可靠性、系统工程、采购、制造等团队紧密合作，共享信息和数据。

数据驱动： 尽可能使用历史数据、测试数据、供应商数据、可靠性预计结果作为输入，减少主观性。

合理假设与记录： 明确记录分配中的所有假设、方法、数据来源及不确定性。

与FMEA/FMECA闭环： 分配结果指导FMEA识别关键项；FMEA的重要性分析(Ei)和故障模式又是分配的重要输入。

平衡艺术： 在可靠性目标、技术可行性、成本、进度、重量等约束间寻求最佳平衡点。

工具支持： 利用可靠性工程软件(如Reliasoft, Isograph)可大幅提高分配、建模、分析的效率和准确性。

 

六、总结

可靠性指标分配绝非简单的数学计算，而是一项融合工程经验、数据分析和系统思维的复杂决策过程。通过科学的方法（如AGREE法）和严谨的流程，将顶层可靠性目标合理分解，能够精准定位设计关键点，优化资源配置，显著提升产品最终达成可靠性目标的概率。

如本案例所示，卫星电源系统通过AGREE分配揭示了PCU是可靠性瓶颈，为设计强化提供了明确方向。同时，分配过程中发现的挑战（如PCU高目标）也促使团队审视系统目标或架构，体现了分配的动态反馈价值。

掌握并有效应用可靠性分配技术，是打造高可靠、高竞争力产品的必经之路，也是工程师从“被动救火”转向“主动设计”可靠性的重要标志。可靠性不是偶然的结果，而是精确分配与严谨设计的必然产物。 每一次科学的分配，都是在为产品的寿命与信任奠定基石。