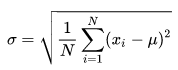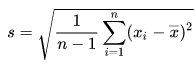标准差是描述数据离散程度的核心统计量,其计算的关键在于根据数据类型(总体或样本)及样本量大小选择合适的分母(n 或 n-1),不同选择直接影响估计结果的准确性。
因此,这里会出现两个公式:
1)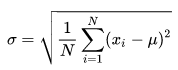
2)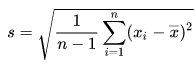
那这两个公式到底哪个对呢?到底用哪一个呢?
先给出答案:两个都对,具体用哪个要看不同的使用场景。
标准差的基础计算逻辑
无论选择何种分母,标准差的计算均以“数据与均值的偏离程度”为核心,核心步骤一致,仅在最终“平均偏离程度”的计算环节存在分母差异,具体流程如下:
1. 计算数据均值:先求出所有数据的算术平均值,作为衡量数据集中趋势的基准;
2. 计算偏差平方和:对每个数据点,计算其与均值的差值,即“偏差”),再将所有偏差平方后求和。这一步的目的是消除偏差的正负抵消,同时放大极端值的影响,符合离散程度的统计意义;
3. 计算“平均偏差平方”:将偏差平方和除以特定分母(n 或 n-1),得到方差;
4. 计算标准差:对结果开平方,得到标准差,其单位与原始数据一致。
分母选择的核心依据:总体数据与样本数据的本质差异
标准差计算中“n”与“n-1”的选择,本质是区分“总体数据”和“样本数据”的统计目的——前者追求“精确描述”,后者追求“无偏估计”。
1. 分母为“n”:总体标准差(或样本中心距)
当我们拥有全部数据(总体)时(例如:某班级50名学生的全部考试成绩、某公司100名员工的全部薪资数据),此时计算的是“总体标准差”,分母使用数据总个数“n”。
逻辑:总体数据的均值是“真实均值”(无误差),偏差平方和除以“n”得到的是“真实的平均偏离程度”,无需修正,结果是对总体离散程度的精确描述。
适用场景:数据覆盖研究对象的全部个体,无“用部分推断整体”的需求;或仅需对现有数据的离散程度做简单描述(如样本中心距),不涉及统计推断。
2. 分母为“n-1”:样本标准差(无偏估计)
当我们仅拥有部分数据(样本)时(例如:从全国1000万中学生中随机抽取500人作为样本、从某品牌10万件产品中抽检200件),此时计算的是“样本标准差”,分母需使用“n-1”(统计学中称为“自由度修正”)。
逻辑:样本均值的偏差会导致标准差低估 样本均值是基于“部分数据”计算的,并非总体的真实均值,其数值会更接近样本中的数据(即“向样本中心靠拢”),导致样本内数据与样本均值的偏差平方和“偏小”——若仍用“n”作为分母,计算出的标准差会低于总体的真实标准差,出现“有偏估计”(低估离散程度)。
而使用“n-1”(自由度=样本量-1,自由度代表数据中“独立可变”的信息数量)进行修正,可放大偏差平方和的平均结果,抵消样本均值带来的低估偏差,使样本标准差成为总体标准差的“无偏估计”(长期多次抽样后,样本标准差的平均值会接近总体真实标准差)。
适用场景:需通过样本数据推断总体特征(如用样本标准差估计总体标准差、进行假设检验、计算置信区间等),是统计学中分析样本数据的“标准方法”。
样本量对分母选择的实际影响
n 与 n-1 的差异程度,会随样本量大小发生显著变化,直接影响计算结果的实用性:
1. 小样本(通常 n ≤ 30):n-1 修正至关重要
当样本量较小时,n 与 n-1 的比例差异较大(例如 n=5 时,n-1=4,差异为25%;n=10时,n-1=9,差异约11%),此时用“n”计算会导致标准差低估问题非常明显,甚至影响后续统计推断的可靠性。
2. 大样本(通常 n > 30):n 与 n-1 差异可忽略
当样本量足够大时,n 与 n-1 的数值非常接近(例如 n=1000 时,n-1=999,差异仅0.1%;n=10000时,差异仅0.01%),此时用“n”或“n-1”计算的标准差几乎相等,低估偏差微乎其微,对统计推断的影响可忽略不计。
3. 从严谨性角度,即使大样本用于推断总体,仍建议优先使用“n-1”。
写在最后
1. 明确数据类型:若为总体数据,分母用“n”,计算总体标准差,描述真实离散程度;若为样本数据(用于推断总体),分母必须用“n-1”,计算样本标准差,确保无偏估计。
2. 关注样本量大小:小样本(n≤30)时,n与n-1的差异对结果影响显著,必须坚持“n-1”修正;大样本(n>30)时,两者差异可忽略,但若涉及统计推断,仍建议使用“n-1”以保持严谨。
3. 区分统计目的:仅需描述现有数据的离散程度(无推断需求),可用“n”;若需通过样本推断总体特征(如估计总体离散程度、进行假设检验),无论样本量大小,均需用“n-1”。